The Peters Wave is a sinusoidal landscape generation technique originally developed by Keith Peters of Bit-101.   figure the construction of the waves begins at the bottom and moves its way up as color, frequency, and amplitude are arbitrarily modified The iterative construction process happens within a single loop, the results of which are immediately visible. Almost every attribute of the landscape is randomly determined. The first value chosen is the number of waves. Typically this is anywhere from 1 to 100. Next, two colors are chosen and the RGB component increments between them are calculated. Finally, the initial amplitudes and frequencies of both the horizontal and vertical waves are chosen.     The random generation of the amplitudes and frequencies is carefully constrained using multiple equations, rather than simple, random +/- increments. Wave amplitudes and frequencies are modified by small amounts, and do not peak or drop out of the stage. The result is an irregular, retreating geometric fold similar to an idealized landscape.     The original code and inspiration for this project was taken directly from Keith Peter's contribution to Fresh Flash, a Friends of Ed publication. The full color spread of irregular purple mountains on pages 4 and 5 compelled me to experiment with these algorithms, a simple, fun escape to imaginative landscapes reminiscent of Fantastic Planet.     figure waves with very small amplitudes and long frequencies   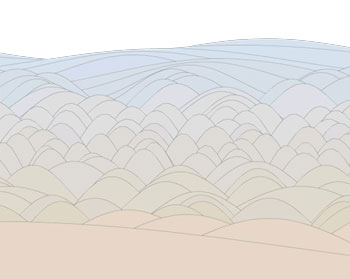  figure waves with higher frequencies in the center only     figure highly regular waves of long frequencies and subtle amplitude     figure wave landscape with some stars           jtarbell, September 2002