The Panton Kurve is a computational construction of a geometric textile named Kurve, originally created by Verner Panton, 1960. There is no user interaction.     Kurve, Verner Panton, 1960.     The Panton Kurve is created by drawing concentric paths around a continually offset epicenter. In this particular example, the Kurve is composed of eight paths of 18 pixels each. figure a. 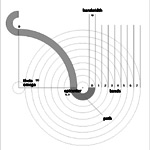geometric deconstruction of the Verner Kurve     figure b. the Kurve design can be broken into smaller path objects. To accurately construct the Kurve while leaving room for later experimentation, the design was broken into small, easily definable pieces. Primarily, this includes the path. The path is an arc of variable radius, width, and color drawn with Flash MX's drawing API. Refer to the diagram at left for details.     The colors of the Panton Kurve were taken from photographs of the original textile pattern. The background was also kept consistent. At the time, Panton's approach to color was considered uncompromising and bold.     We might construct something a little more irregular than the original Kurve if we choose not to restrict the path increments to 90 degrees. Instead, we will allow rotations from as small as 30 degrees to as large as 330 degrees. Figure c. implementation details using arbitrary angles for the path objects     The Kurve and variations thereof, became a ubiquitous component in Verner Panton's work. I believe the success of this geometric design is owed to its harmonious ability to flow from one focal point to another. By most observers, the Panton Kurve is unconsciously regarded as good. View another Panton inspired computation, Geometri' I.                 jtarbell, february 2003