Simple recursive construction of a space filling triangle. There is no user interaction. For any given triangle ABC, pick a random midpoint D and divide into three smaller triangles, so that triangles ADC, ABD, and DBC now exist. Repeat the procedure for each of the new triangles.   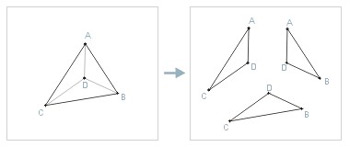figure a. the triangular substitution model of Triangulation     The resulting computational structure is nested in nature. Triangle points closer to the beginning of the sequence are highlighted by glowing rays. This is because they are shared by larger number of child triangles. The graphic representation of this process uses a single movieclip for all three triangle divisions. When a triangle is divided, a Movieclip is placed at the origin of the stage and instructured to draw segments DA, DB, and DC. Drawing the triangle this way avoids the overlapping borders caused by drawing the perimeter. A maximum recursive depth of 8 calls is enforced to keep the structure reasonable.                 jtarbell, march 2003